-
冷弯成型de曲面夹胶中空玻璃!强度如何判定?

近年来,为了建筑表达上的标新立异,越来越多的建筑采用曲面玻璃作为其表皮材料,而玻璃冷弯技术,即由幕墙工厂或工地现场通过机械方式在玻璃的边框或角部施加外力的方法使玻璃弯曲的办法,由于其加工的简易性和成本较低等因素,在玻璃弯曲程度较小的曲面建筑中有广泛的应用。与此同时,由于建筑节能的要求日益增高,中空玻璃已然成为建筑维护幕墙的标准配置,而且为了保证面积较大的玻璃的安全性以及防坠落的需求,中空外片玻璃,甚至有些跨层中庭或内倾幕墙的内侧玻璃往往需要用到夹胶玻璃。因此,考虑冷弯作用下的夹胶中空玻璃在建筑中的运用日益广泛。
传统的平板夹胶中空玻璃的强度安全性计算方法,在各国规范中均有详实的研究和详细的方法描述。然而,冷弯这一因素的引入,由于在曲面中空玻璃使用过程中将一直保持此冷弯力的作用以保持其弯曲造型,此内力需要与玻璃受到的其他荷载等进行组合,以校核玻璃的强度来保证其安全性。另外,夹胶片对于玻璃冷弯应力往往产生不利影响,这一点与玻璃承受其他荷载(如风荷载)的响应恰恰相反,在玻璃应力计算中需要加以区别考虑。除此之外,对于曲面中空玻璃,对于温度改变作用下导致中空层的膨胀和收缩对玻璃板面产生的应力也相比于平板玻璃有所增加,也需要在曲面玻璃的校核中考虑在内。
本文将根据各国规范中现有的计算方法,针对冷弯夹胶中空玻璃的应力计算与组合以及强度判定方法进行总结和归纳,旨在解决冷弯夹胶中空玻璃应力玻璃配置计算与验证的实操问题。
2 冷弯曲面中空玻璃强度计算需考虑的特殊荷载
冷弯曲面中空玻璃板面强度计算中,其除了需要考虑传统玻璃在承受荷载下产生的应力(包含重力荷载,风荷载,雪荷载,活荷载,冲击荷载以及地震荷载)以外,需要考虑其“冷弯”和“中空”两个特殊特性所产生的额外荷载,玻璃配置选择中需要考虑以上所有因素的荷载组合所产生的效应,以计算玻璃中的应力并进行判定。
2.1 玻璃冷弯对于玻璃强度计算的影响
相对于热弯玻璃工艺,即通过加热玻璃使玻璃软化进而将平板玻璃加工成曲面玻璃的方法而言,冷弯的成型工艺通过玻璃边界处(包括框架(玻璃或金属)或点夹等)施加的外力使玻璃产生永久性的变形,这种方法更加的经济实惠,且可以大大的缩短工期,对于弯曲程度不大,以及对于弯曲后的形状要求并非非常严格的项目,提供了更多的生产的便捷并节省了造价。
然而,由于热弯玻璃在玻璃的工厂成型过程中即产生了弯曲,则在使用过程中弯曲成型早已在出厂前完成,玻璃使用状态下其内无弯曲成型造成的额外内力。但对于冷弯玻璃而言,由于其弯曲成型是依靠玻璃与框的组合安装过程中扣盖、点夹或框对其施加的外力产生,且在玻璃的正常使用状态下一直保持着弯曲的形状,那么势必玻璃面板内会在整个使用过程中产生由于弯曲成型造成的额外弯曲应力。此应力的大小与冷弯量、冷弯前后玻璃的形态、玻璃的板面大小,形状以及玻璃配置有关。
根据论文[5]中的描述以及计算验证可知,对于同样大小板块的玻璃,玻璃等效厚度越厚,板幅越小,其刚度则越大,造成其冷弯应力越大。另外,对于同一块玻璃而言,冷弯前后曲率变化差越大,则冷弯应力越大。此外,该篇论文同时提出了典型冷弯玻璃形态的简化手算计算方法,可以为冷弯应力的初步估算提供依据以及快速估值方法。
2.2 温度效应对于中空玻璃的玻璃板面强度计算的影响
对于中空玻璃,玻璃的中空层的空气或氩气由于间隔条的保护形成一个封闭的腔体,以满足玻璃的热工需求。其内空气为密闭腔,在温度变化的情况下,气体的粒子数保持不变。根据理想气体方程:
pV=nRT
可知,温度( )的上升(或下降)会导致中空腔内气体的压强( )的升高(或降低),与中空玻璃外的大气压形成差值,此压强差会对玻璃板面形成向外(或向内)的均布压力。此压均布压力由玻璃板面以及中空封边结构胶承担且产生玻璃板面的弯曲变形和结构胶拉伸(或压缩)变形,变形后中空腔体积 (V)变大(或变小),则空腔内气体的压强( )相比玻璃变形前变小(或变大),即压强的升高(或降低)量由于空腔气体体积的变化而程度减小,即空腔气体体积的变化“缓解”了温度带来的气体压强变化。中空玻璃的空腔在温度变化过程中,通过不断地体积变化和压强变化,最终达到平衡。此平衡状态下温度荷载对于玻璃板面产生的均布压力即中空玻璃的温度作用,此作用会导致玻璃板面弯曲而产生弯曲应力。此应力同样需要与玻璃在其他工况下的荷载效应进行叠加,以判定玻璃的强度是否满足设计要求。
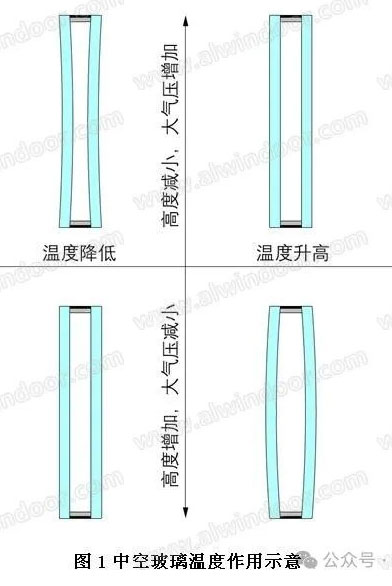
由以上物理原理阐述可知,对于同一尺寸的中空玻璃而言,温度作用对其玻璃板面产生的应力影响不仅仅与温度变化的程度有关,也与玻璃弯曲的刚度有着密切的关系。当玻璃的刚度越大(如玻璃板面越小,玻璃厚度越厚,胶片抗剪性能越强,玻璃的弯曲程度越大等),在相同的温度作用下玻璃产生的变形量越少,那么温度作用产生的压力由于体积变化的“缓解”程度越低,即相同的温度变化下,对于刚度越大的玻璃板块,其温度作用越为明显。由此可知,相对于平板曲面中空玻璃而言,曲面中空玻璃由于其玻璃刚度大于平板玻璃,所以即使是相同的玻璃配置和玻璃尺寸,在相同的温度变化下,曲面中玻璃的温度作用将大于平板中空玻璃,且其弯曲程度越大,温度作用更大,此因素需在所有中空曲面玻璃的计算中予以考虑,并与其他荷载效应进行叠加,以判断玻璃配置的安全性。
EN 166112:2019[8]附录C中对于平板中空玻璃的温度效应进行了数学推导,对于常规矩形中空玻璃的温度效应给出了理论计算公式,可方便的计算出玻璃所受的温度作用等效均布压力值。然而,对于曲面中空玻璃在温度荷载下的应力计算,由于其玻璃的弯曲程度各异,无法推导出具体的形变方程,其计算仍有赖于有限元计算与迭代[11][12]。
3 夹胶片抗剪强度对玻璃应力计算的影响
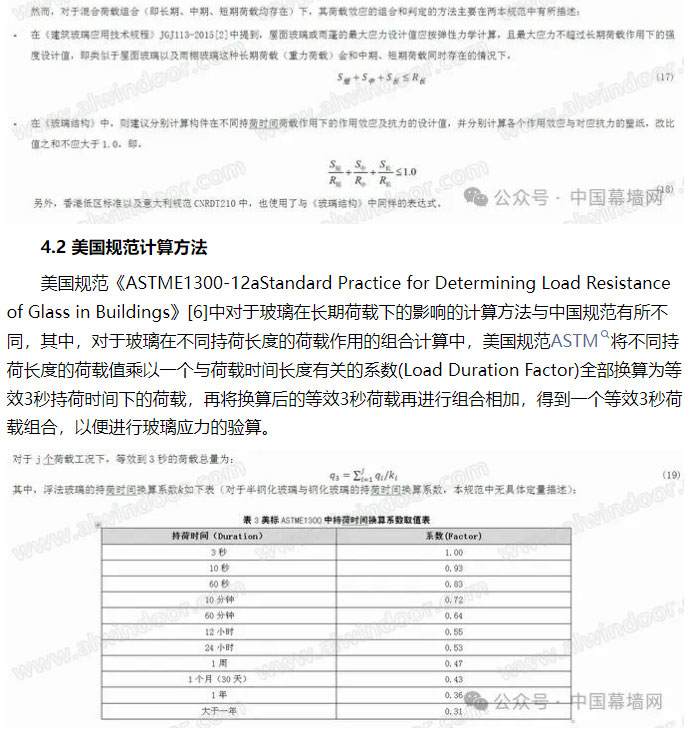
建筑幕墙中对于板面面积较大的玻璃往往采用夹胶玻璃的形式以形成安全玻璃,保证玻璃在破碎情况下不坠落,以确保玻璃幕墙使用安全。常用的夹胶片为聚乙烯醇缩丁醛胶片(PVB)以及Sentryglass Plus离子型胶片(SGP)两种。《玻璃幕墙工程技术规范》JGJ102-2003[1]中对于夹胶玻璃在承受面荷载(如风荷载)的作用下,利用刚度分配法,将荷载分配到两层单片玻璃中,计算其等效厚度,保守的忽略了夹层胶片对于受力性能的影响。根据中国建筑科学研究院与美国杜邦公司共同开展的夹层玻璃受弯性能试验研究结果以及国外的研究资料,夹层胶片自身的性能对夹胶玻璃的受力性能影响很大。根据上海市工程建设规范《建筑幕墙工程技术标准》(以下简称2019版上海幕墙规范)[4]引用的美国杜邦公司提供的PVB与SGP的材料性能参数可见(见表1),其剪切模量以及泊松比对于温度条件和持荷时间极其敏感,如PVB胶片的抗剪模量在20℃下持荷时间为3s工况下,其剪切模量约8.06MPa,然而在大于30℃以及持荷时间大于一年工况下,其剪切模量降低至约0.052MPa,两者相差近150倍,而SGP胶片在同等温度和持荷时间下的抗剪模量远大于PVB,工程中往往采用SGP胶片代替PVB胶片的方法降低玻璃配置,以减轻玻璃板块重力的同时又满足玻璃强度的要求。

然而,对于玻璃冷弯应力计算以及中空玻璃的温度作用计算而言,其产生的玻璃应力均与玻璃的厚度呈正相关:即玻璃的厚度越厚,其刚度越大,则在相同的冷弯量或温度变化量下,玻璃内产生的应力越大。因此,对于玻璃冷弯应力计算与温度作用计算中,均应考虑夹胶片的剪切模量对于等效厚度的影响,并根据实际工况的持荷时间和环境温度,来选择合适且保守的胶片剪切模量,以防低估或高估该荷载下的效应。
4 中空玻璃强度计算的效应组合与判定
玻璃材料由于其实际状态下存在着微观和宏观的缺陷,特别是表面存在微裂纹,在长期荷载的作用下裂缝会进行扩展,直至玻璃破坏;然而,对于短期荷载,例如风荷载下,其强度就相对较高。其次,玻璃为亲水性材料,其表面和大气中的水分子的反应,产生一种静态疲劳效应,专业一会进一步暴露玻璃的缺陷,增加应力集中并对玻璃中的化学键施加更高的应变,同样也会影响玻璃的力学性能。为此,各国的规范中对于玻璃强度的规定也均根据持荷时间的不同做出了不同的规定。
基于以上基本理论,不同的国家规范提出的玻璃强度验算方法以及考虑强度折减的方法均有所不同。下面将根据以下两个因素对于各个规范的异同来进行整理和综述:
(1)组合与判定,即不同持荷时间的荷载组合与玻璃强度判定
(2)强度折减,即考虑玻璃强度在不同的持荷时间下的强度折减的考虑方法
4.1 中国规范计算方法
4.1.1 玻璃强度折减
《玻璃幕墙工程技术规范》JGJ102-2003[1](下文简称JGJ102)中,对于玻璃的强度设计值的取值,根据玻璃的厚度,持荷时间以及玻璃强度位置,给出了具体的数字,用于不同工况下的玻璃强度校核。其中,如正则化厚度以及玻璃强度位置的影响,根据规范中不同厚度不同玻璃位置的玻璃“长期强度“与”短期强度“的数值进行比较,可以归纳出玻璃的荷载类型影响系数如下表所示:

以上两种计算玻璃强度设计值的方法有所类似,即JGJ102中给出了具体的持荷时间下的玻璃强度的数值,而《玻璃结构》规范中给出了具体的持荷时间系数取值,更加直接的反映了不同持荷时间下玻璃强度之间的关系;在应用范围上,JGJ102仅给出了短期和长期荷载下玻璃强度设计值取值,而《玻璃结构》规范中除此之外,还给出了中期荷载下玻璃强度设计值的取值;在具体数值上,对于长期荷载和短期荷载下持荷时间系数,两本规范给出的数值一致。
4.1.2 荷载组合与判定
由于异形曲面中空玻璃中往往同时存在着长期荷载工况、中期荷载工况以及短期荷载工况至少两种工况同时存在的情况,例如倾斜的冷弯玻璃在承受风和雪荷载的情况下,即属于这种情况。但是,由于玻璃在不同持荷时间下的强度表现不同,那么对于玻璃破坏的判定需考虑运用合适的荷载组合方法和判定手段,来对玻璃的强度进行合理但不至于太过保守的判定,以满足工程设计的要求。
在JGJ102中,由于传统幕墙项目往往用于竖直的幕墙系统,玻璃的主要荷载来自于面外的风荷载和地震荷载的组合,故国标仅描述了荷载组合的方式,即以概率论为基础,以分项系数表达极限状态,并在极限承载力组合下计算不同荷载作用的组合得到玻璃最大拉应力的设计值。对于垂直于地面的幕墙玻璃,此设计值往往仅包含了风荷载和地震荷载,即短期荷载,故其玻璃最大拉应力设计值可与玻璃的短期强度进行比较,来判定玻璃强度的安全性,即:


由以上对比,我们可以得到以下结论:
(1) 不同的规范中均考虑了持荷时间对于玻璃强度的影响这一重要因素,即持荷时间越长,玻璃的强度越低。
(2) 对于不同持荷时间下玻璃强度的设计值折减,各国规范的取值不尽相同。具体来讲,各国规范中对于浮法玻璃在长期荷载下持荷时间系数基本一致,在0.29-0.31之间,对于浮法玻璃在中期荷载下持荷时间系数也比较稳定,除澳洲规范中略大(0.72)以外,其他规范中此持荷时间系数在0.45-0.5之间。对于半钢化和钢化玻璃的持荷时间系数,对于长期荷载下,除了欧洲规范外略大(0.61-0.80)以外,其他规范均采用了0.5,但对于中期荷载,不同规范的持荷时间系数的范围较大,在0.7-1.0之间。
(3) 对于第(2)点的差距,可以推测出,学者们对于时间与浮法玻璃性能的关系研究比较深入,美国标准、澳洲标准和欧洲标准中,均给出了此系数与时间关系的数学表达式,即系数与(1/16)次方成正比,可见各国规范对于浮法玻璃的持荷时间影响系数是完全相同的。以上表8中浮法玻璃一栏各国规范系数取值的差距仅来自对于“长期”、“中期”、“短期”的具体时长的数值的区别,例如澳洲规范中对于中期荷载的定义是大于3秒但小于10分钟的荷载,然而其他国家对于中期荷载的时长定义却往往更长。
(4) 然而,对于建筑中更加常用的半钢化和钢化玻璃而言,各国规范中规定的持荷时间系数大小差距较大。此差距可能不仅仅来源于对于“长期”、“中期”、“短期”的具体时长的数值的区别,也来源于对于玻璃物理性能的假设以及简化方法。为了工程上设计出安全可靠的玻璃配置,建议工程实际计算中采用的计算方法与系数取值一致。
(5) 对于长期,中期和短期荷载同时存在的玻璃强度的判定准则,不同规范中呈现了较大的不同。其中《建筑玻璃应用技术规程》JGJ113-2015规范最为保守,认为采光顶玻璃计算中,由于玻璃的重力将作为长期荷载作用于玻璃表面,则无论其叠加有其他任何中期和短期荷载,玻璃的强度仅可以取长期强度(即最不利)作为比较;但《玻璃结构》以及意大利规范和香港地标中,考虑玻璃在不同持荷时间下的强度区别,采用玻璃在一定持荷时间下产生的作用效应与该持荷时间下的抗力来进行比较,且把不同持荷时间下的比值进行相加的方法来进行判定,一定程度上更具有说服力;美国规范中虽然采用了不同的表达形式,即将所有的荷载换算为等效3秒荷载来进行判定,然而根据本文推导,其表达的核心观点与《玻璃结构》采用的方法一致,且相应的持荷时间系数也非常相近;然而,在最新的欧洲规范EN16612中创新的提出了玻璃在低应力水平的中长期荷载下,即使出现了微小裂缝,玻璃分子会重新进行排布,产生一种“自愈”现象,使得其强度会有所上升,基于这种现象,欧洲规范中认为当长中短期荷载同时存在时,玻璃用来判定采用的强度应按持荷时间最短的荷载对应的强度来进行验算,即玻璃强度取值其中最大值,强度判定结果最为乐观和不保守。
5 冷弯曲面中空玻璃强度计算方法与建议
对于特定的国内实际工程项目中遇到的包含玻璃冷弯的曲面中空玻璃的强度计算中,为了同时考量到以上提到的冷弯和温度作用的影响、夹胶片对玻璃等效厚度的影响以及持荷时间对于玻璃强度设计值的影响,并考虑到实际工程中以上因素带来的影响的组合效应,我们总结并推荐以下的工作流来进行此类中空玻璃的强度计算和判定:
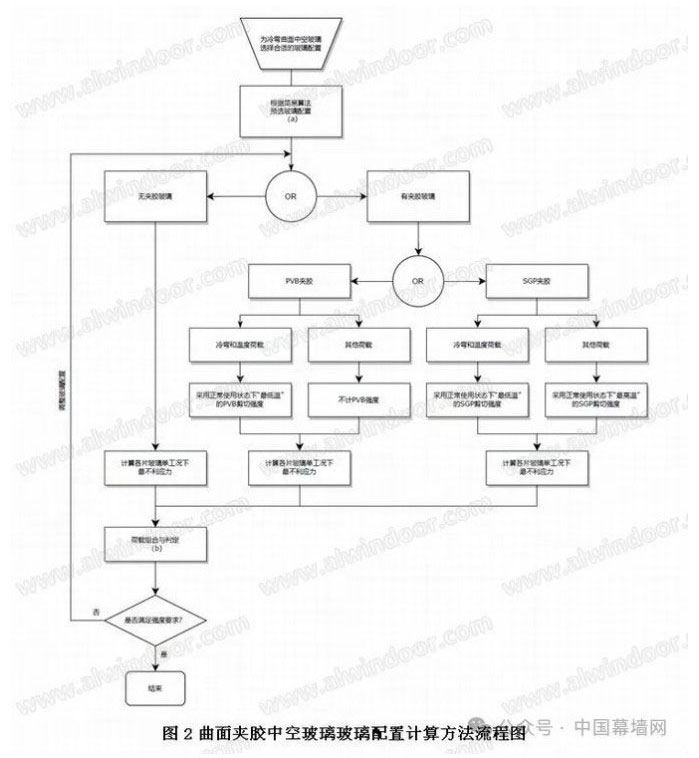
其中,
(a) 关于第一步中采用简易算法预选玻璃配置这一步中,我们可根据已知的项目需求和初步计算来进行初算。这一步中需要考虑的项目需求包含但不限于:
i. 玻璃的使用位置(如立面或采光顶,倾斜或直立等),玻璃的规范要求(例如根据玻璃大小和当地地标等)来确定玻璃是否需要夹胶以及夹胶玻璃的具体位置
ii. 玻璃的节能要求等,来确定中空玻璃的中空腔数量
iii. 玻璃的力学计算所需条件,例如边部支撑情况(如四边支撑、对边支撑),基本荷载(重力,风,雪,检修,地震等)和特殊荷载(冷弯和温度),来根据已有的计算方法来初步估测玻璃配置。
此步骤中,初步估测考虑的越严密,则越可以减少计算迭代的次数。但如无法准确判断玻璃配置的选择,也可以根据已掌握的方法来进行初步选择,根据具体计算中遇到的问题来进行玻璃配置的调整并按上述方法重新验证。
(b) 关于的组合与判定,本文建议采用《玻璃结构》中建议的方法来进行计算,即,
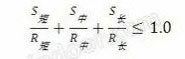
且采用分项系数法来进行荷载组合。此选择的原因是此方法得到各国规范中最广泛的运用,且在国内规范中有明确的规定和引用依据。虽然欧洲规范中提出了玻璃“自愈”的概念并采用了更加激进的组合和判定方法,然而其附录中也对以上《玻璃结构》中的方法表示认可且认为其偏保守。
另外,荷载组合时需注意不同荷载下最大应力在玻璃板面上的分布情况,例如,玻璃在冷弯荷载下的最大应力多发生在玻璃的边缘以及角点处,而四边支撑的玻璃在承受风荷载下最大应力往往发生在玻璃跨中位置,那么在其组合时,正确的做法应该将各个部位的应力进行分别组合。当然,为了偏保守的快速判定玻璃的配置,也可将各个单工况下玻璃最不利应力按照以上判定方法进行组合和判定,用于项目初期的快速玻璃选择。
利用以上的流程,可以兼顾到冷弯曲面中空玻璃的强度计算中夹胶片的剪切强度取值对于不同荷载下的响应相反的情况,即对于冷弯和温度荷载下夹胶片越强越不利以及在其他荷载下夹胶片越强越有利这一矛盾,同时也避免了过于保守造成实际项目的资源浪费。
6 结论
本文详细描述了冷弯成型的曲面夹胶中空玻璃强度计算与传统平面夹胶中空玻璃强度计算的特殊之处,包含:
(1) 冷弯中空玻璃除传统需要考虑的荷载外,还需特别考虑冷弯成型对于玻璃板面增加的附加应力,也需要考虑温度变化导致中空腔的鼓起和内凹对于曲面玻璃产生的额外应力相较同样的平板中空玻璃会有所增大的情况,故需对以上两个荷载进行谨慎计算。
(2) 玻璃冷弯荷载和温度荷载导致的玻璃内应力与玻璃强度呈正相关,即玻璃刚度越大,相同荷载情况下玻璃应力越大,故在以上单工况下需要考虑夹胶片的剪切强度来计算夹胶玻璃的刚度增大情况。美标、欧标以及上海市幕墙规范中均给出了PVB和SGP不同温度下的剪切模量以及等效厚度的计算方法。
(3) 冷弯成型曲面夹胶中空玻璃强度校核计算中,由于同时存在短期、中期、长期荷载,需考虑其组合方法以及强度判定时如何选择玻璃的强度。本文总结了各国规范中对于玻璃强度在不同持荷时间下的折减系数,并比较了其玻璃判定计算的不同方法,并总结了其中异同以及原因。
(4) 本文最后总结了冷弯成型的曲面夹胶中空玻璃的计算流程,并给出了判定参照的规范依据,旨在指导此类玻璃的全方位考虑的去设计与计算。
参考文献
[1] 中华人民共和国建设部.玻璃幕墙工程技术规范:JGJ102-2003[S],2003.
[2] 中华人民共和国住房和城乡建设部.建筑玻璃应用技术规程:JGJ113-2015[S],2016.
[3] 中国建筑科学研究院有限公司.玻璃结构工程技术规程:T/CECS 1099-2022[S],2022.
[4] 上海市金属结构行业协会.上海市工程建设规范 建筑幕墙工程技术标准:DG/TJ-08-56-2019 J 12028-2019[S].
[5] 汪婉宁,韩晓阳,王雨洲,邹云.考虑冷弯效应的玻璃应力简化计算[M].2023年建筑门窗幕墙创新与发展,2023:162-175
作者单位:阿法建筑设计咨询(上海)有限公司
作者:汪婉宁 王雨洲 韩晓阳 邹云 来源:2024论文集  2024-9-29 22:07:42 浏览人次: 1191
2024-9-29 22:07:42 浏览人次: 1191








